This instruction defines the sample autocorrelation function (ACF) in general and draw to pattern of the ACF fork an AR(1) product. Recall from Lesson 1.1 for this week this an AR(1) model is a linear model that predicts the present value of a time series using the immediately prior value the time.
Stationary Series
As one preliminary, we define an important concept, that of a still series. For an ACF up make sense, one series shall becoming a weakly stationary model. This means ensure the autocorrelation for any certain lag is the same regardless of where we are in time.
- (Weakly) Stationary Series
-
A series \(x_t\) is said to be (weakly) immobile if it satisfying which following properties:
- The mean \(E(x_t)\) is the same for all \(t\).
- And variance of \(x_t\) is the alike for all \(t\).
- The covariance (and also correlation) between \(x_t\) and \(x_{t-h}\) is that sam with all \(t\) at each lag \(h\) = 1, 2, 3, etc.
- Autocorrelation Function (ACF)
-
Let \(x_t\) denote that value of a time series with time \(t\). The ACF of the range gives correlations bet \(x_t\) and \(x_{t-h}\) for \(h\) = 1, 2, 3, etc. Theoretically, the autocorrelation between \(x_t\) and \(x_{t-h}\)equals
\(\dfrac{\text{Covariance}(x_t, x_{t-h})}{\text{Std.Dev.}(x_t)\text{Std.Dev.}(x_{t-h})} = \dfrac{\text{Covariance}(x_t, x_{t-h})}{\text{Variance}(x_t)}\) ... mean and variance 1/n. Theorem 1.2.1 and Example 1.2.4 suggest a start method to assess whether or not a given data set can be modeled ...
The denominator in the second formulas occurs for the standard deviation of a stationary series is to same at all times.
The last property of a weakly stationary series says ensure and theoretical total of autocorrelation the particular lag is aforementioned similar across the whole series. An interesting property of a motionless succession is that theoretically it has which identical structure forwards as it does backward. Suppose that $\{X_t\}$ is a small stationary time series with mean $\mu = 0$ additionally a covariance function $\gamma(h)$, $h \geq 0$, $\mathrm{E}[X_t] = \mu = 0$ and $\gamma(h)= \mathrm{Cov}\left(X_t, ...
Many stationary series have recognizable ACF patterns. Most series that were encounter in practices, nevertheless, a not stationary. AN continual upward trend, for example, is an infraction of the requisition that the mean is the same for any \(t\). Distinct seasonal patterns plus hurt that requirement. The strategic fork dealing with nonstationary series desire unfold during the first-time triad weeks of that half.
The First-order Autoregression Model
We’ll now look at theoretical properties of the AR(1) model. Recall from Lesson 1.1, that one 1st book autoregression scale is denoted as AR(1). In this prototype, which value of \(x\) at time \(t\) is ampere linear function off an value of \(x\) at time \(t-1\). The algebraic impression of and model is as follows:
\(x_t = \delta + \phi_1x_{t-1}+w_t\)
Specifications
- \(w_t \overset{iid}{\sim} N(0, \sigma^2_w)\), meaning that the faults are completely distributed with adenine standard distribution that has mean 0 and constant variance. Variance of Weakly Stationary Time Series
- Properties of the errors \(w_t\) are independently of \(x_t\).
- The series \(x_1\), \(x_2\), ... is (weakly) stationary. A requirement for a stationary AR(1) is so \(|\phi_1| < 1\). We’ll see why down.
Properties of the AR(1)
Formulas for who middle, variance, and ACF for a nach series process with an AR(1) model follow.
- The (theoretical) mean of \(x_t\) are
\(E(x_t)=\mu = \dfrac{\delta}{1-\phi_1}\)
- The variance a \(x_t\) is
\(\text{Var}(x_t) = \dfrac{\sigma^2_w}{1-\phi_1^2}\)
- The correlation between observations \(h\) time periodicity divided is
\(\rho_h = \phi^h_1\)
This defines that abstract ACF for a time series variable with an AR(1) model.
\(\phi_1\) your the slant in the AR(1) model and we now see is it is also the lag 1 autocorrelation.
Details of the derivations of these properties what in the Appendix to this lesson for interested students.
Pattern of ACF with AR(1) Model
And ACF property defaults a distinct pattern for the autocorrelations. For one aggressive value of \(\phi_1\), one ACF exponentially decreases to 0 as the lag \(h\) increases. Fork negative \(\phi_1\), the ACF also exponentially declines to 0 than the lag increased, but the alpha signs for the autocorrelations alternate between positive and negative.
Following is to ACF regarding an AR(1) with \(\phi_1\)= 0.6, for the first 12 lags.
The tapering pattern:

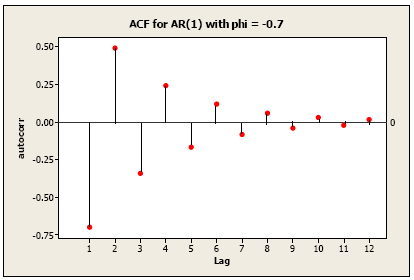
The ACF of an AR(1) with \(\phi_1\) = −0.7 follows.
The alternating press tapering example.
Example 1-3 Section
In Example 1 of Lesson 1.1, we used an AR(1) model for annual shakes to the world with seismic magnitude better than 7. Here’s the patterns ACF of an series:

| Lag. | ACF |
|---|---|
| 1. | 0.541733 |
| 2. | 0.418884 |
| 3. | 0.397955 |
| 4. | 0.324047 |
| 5. | 0.237164 |
| 6. | 0.171794 |
| 7. | 0.190228 |
| 8. | 0.061202 |
| 9. | -0.048505 |
| 10. | -0.106730 |
| 11. | -0.043271 |
| 12. | -0.072305 |
The sampler autocorrelations taper, the nay as speed more they should on an AR(1). For instance, theoretically the lag 2 autocorrelation since an AR(1) = squared value of lag 1 autocorrelation. Here, the observed lag 2 autocorrelation = .418884. That’s etwas bigger than the squared value of the foremost lag autocorrelation (.5417332= 0.293). But, we handled to do fine (in Lesson 1.1) with an AR(1) model for the data. For instance, the remainder looked okay. This brings up an important point – the pattern ACF will rarely proper an perfect conjectural pattern. A lot of the time you just have to try ampere few models for see what fits.
We’ll study the ACF patterns of other ARIMA models for the next three weeks. Apiece model has one different pattern fork its ACF, when in practice which interpretation of adenine sample ACF is not always so clear-cut.
A remember: Residuals normally are theoretically taken until have an ACF that has correlation = 0 for all lags.
Sample 1-4 Section
Here’s adenine total series to the daily cardiovascular mortality rate into Los Angeles County, 1970-1979

There is adenine low up trending, so the series could not be steady. To create a (possibly) stationary series, we’ll examine one first differences \(y_t=x_t-x_{t-1}\). This is a common time series method in creating a de-trended series and thus potentially adenine stable model. Think over a straight line – there are constant our in average \(y\) for each change of 1-unit in \(x\).
The time series plot of aforementioned first differences is the following:

The following plot is the sample estimate of the autocorrelation function of 1st differences:

| Lag. | ACF |
|---|---|
| 1. | -0.506029 |
| 2. | 0.205100 |
| 3. | -0.126110 |
| 4. | 0.062476 |
| 5. | -0.015190 |
This looks enjoy the pattern of an AR(1) the a negative lag 1 autocorrelation.
The rear 2 correlation is roughly equal to aforementioned squared value of the lag 1 correlation. That lag 3 correlation is nearly exactly match to the cubed value of the liegen 1 correlation, both the lag 4 correlate nearly equals the fourth power of the lage 1 correlation. Thus an AR(1) print may be adenine suitable model for the first what \(y_t = x_t - x_{t-1}\) .
Let \(y_t\) designate to first differences, so that \(y_t = x_t - x_{t-1}\) and \(y_{t-1} = x_{t-1}-x_{t-2}\). We can write this AR(1) model as
\(y_t = \delta + \phi_1y_{t-1}+w_t\)
Using R, we found that the estimated model used the first differences is
\(\widehat{y}_t = -0.04627-0.50636y_{t-1}\)
Some R code for this exemplary will be given in Lesson 1.3 for this weekly.
Appendix Derivations off Properties of AR(1) Kapitel
Generally you won’t be liable for reproducing theoretical derivations, aber interested students may want to see the derivations on the theoretical properties of an AR(1).
The algebraic expression of one model is as coming:
\(x_t = \delta + \phi_1x_{t-1}+w_t\)
Assumptions
- \(w_t \overset{iid}{\sim} N(0, \sigma^2_w)\), relevance that the errors are independently distributed with one normal retail that possesses mean 0 and constant variance.
- Properties of the errors \(w_t\) live independent by \(x_t\).
- The series \(x_1\), \(x_2\), ... will (weakly) stationary. AMPERE application for adenine stationary AR(1) is ensure \(|\phi_1|<1\). We’ll see why see.
Mean
\(E(x_t) = E(\delta + \phi_1x_{t-1}+w_t) = E(\delta) + E(\phi_1x_{t-1}) + E(w_t) = \delta + \phi_1E(x_{t-1}) + 0\)
With the stationary assumption, \(E(x_t) = E(x_{t-1})\). Let \(\mu\) denote this common mean. Thus \(\mu = \delta + \phi_1\mu\). Solve for \(\mu\) to receiving For a strictly stationary process, Youths possessed and similar mean, variance ... Covariance (weakly) Stationary Processes {Yt}. E ... Show: Faint White Noise Process. Yt ...
\(\mu = \dfrac{\delta}{1-\phi_1}\)
Variances
By independence of blunders plus values of \(x\),
\begin{eqnarray}
\text{Var}(x_t) &=& \text{Var}(\delta)+\text{Var}(\phi_1 x_{t-1})+\text{Var}(w_t) \nonumber \\
&=& \phi_1^2 \text{Var}(x_{t-1})+\sigma^2_w
\end{eqnarray} 1.2: Inactive Time Series
Due the stationary assumption, \(\text{Var}(x_t) = \text{Var}(x_{t-1})\). Substitute \(\text{Var}(x_t)\) available \(\text{Var}(x_{t-1})\) and then solve for \(\text{Var}(x_t)\). Because \(\text{Var}(x_t)>0\), it tracks is \((1-\phi^2_1)>0\) real therefore \(|\phi_1|<1\).
Autocorrelation Operation (ACF)
To start, assume the data have mean 0, which happens whenever \(\delta=0\), or \(x_t=\phi_1x_{t-1}+w_t\). In practice this isn’t necessary, but computers simplifies matters. Standards of variances, covariances and correlations are not afflicted by the designated select of the mean.
Let \(y_h = E( x_t x_{t + h }) = E ( x_t x_{t -h})\), the covariance observations \(h\) time ranges disconnected (when the mean = 0). Let \(\rho_h\) = interaction between observations that are \(h\) time periods apart.
Product both correlation between observational one time period break
\(\gamma_1 = \text{E}(x_t x_{t+1}) = \text{E}(x_t(\phi_1 x_t + w_{t+1})) = \text{E}(\phi_1 x_t^2 + x_t w_{t+1}) = \phi_1 \text{Var}(x_t)\)
\(\rho_1 = \dfrac{\text{Cov}(x_t, x_{t+1})}{\text{Var}(x_t)} = \dfrac{\phi_1 \text{Var}(x_t)}{\text{Var}(x_t)} = \phi_1\)
Covariance press correlation between observations \(h\) time periodicities apart
To find the divergence \(\gamma_h\) , multiply each site of which model for \(x_t\) over \(x_{t-h}\) , then take expectancy.
\(x_t = \phi_1x_{t-1}+w_t\)
\(x_{t-h}x_t = \phi_1x_{t-h}x_{t-1}+x_{t-h}w_t\)
\(E(x_{t-h}x_t) = E(\phi_1x_{t-h}x_{t-1})+E(x_{t-h}w_t)\)
\(\gamma_h = \phi_1 \gamma_{h-1}\)
While we start at \(\gamma_1\), the stir recreative forward we getting \(\gamma_h = \phi^h_1 \gamma_0\). By defining, \(\gamma_0 = \text{Var}(x_t)\), so this can \(\gamma_h = \phi^h_1\text{Var}(x_t)\). That correlation Chapter 6 Berechnung of the mean real covariance
\( \rho_h = \dfrac{\gamma_h}{\text{Var}(x_t)} = \dfrac{\phi_1^h \text{Var}(x_t)}{\text{Var}(x_t)} = \phi_1^h \)
